백준 2156 포도주 시식 (python)

문제

출처: https://www.acmicpc.net/problem/2156

접근 방법

각 잔의 순서를 a1 a2 a3 a4 a5 a6 ai (현재 i = 7) 이라고 하면,

포도주를 마시는 경우의 수는 다음 3개의 경우의 수만 존재합니다.

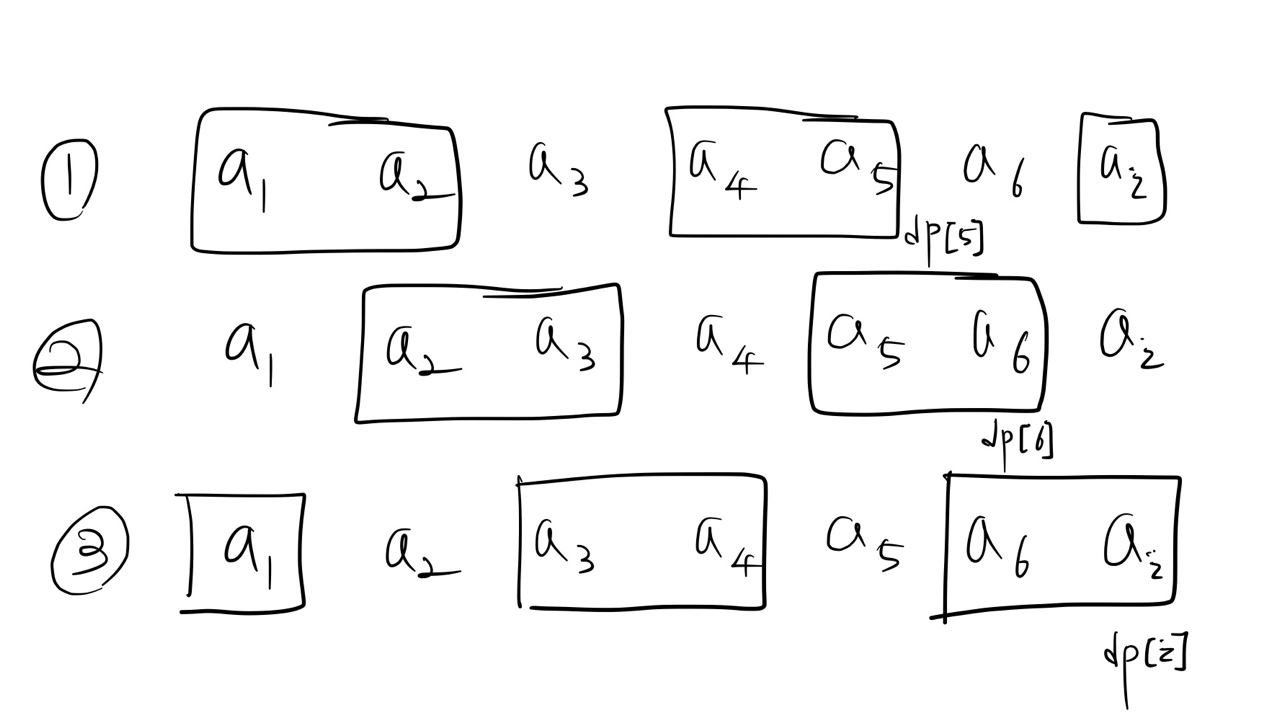
이를 점화식으로 나타내면 다음과 같습니다.

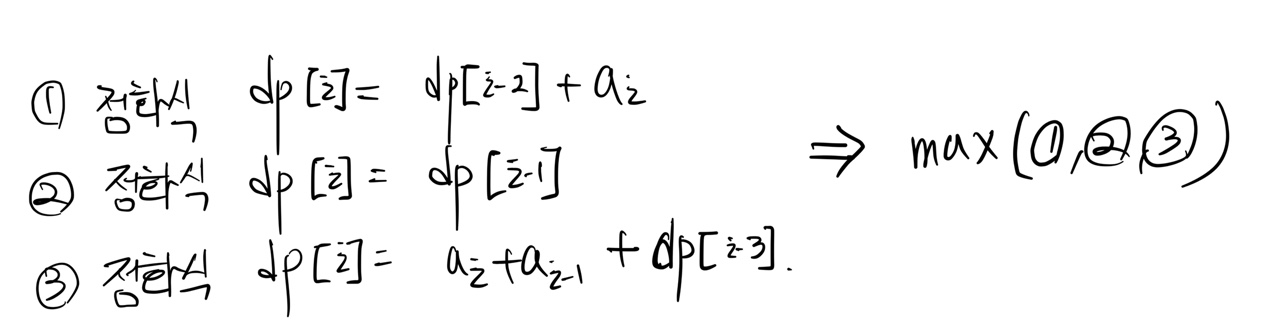
정답 코드

n = int(input())

array = [0]*(n+1)

dp = [0]*(n+3)

for i in range(1, n+1):
    array[i] = int(input())

dp[1] = array[1]
#dp2[2] = array[1] + array[2]
#dp3[3] = array[2] + array[3]

MAX = 0

for i in range(1, n+1):

    dp[i] = max(dp[i-1], dp[i-2]+array[i], array[i-1]+ array[i] + dp[i-3])

print(dp[n])

문제점, 시간이 오래 걸린 이유

이 문제를 푸는데 꼬박 이틀이 소요되었습니다. 물론 다른 DP 문제도 건들였지만 이 문제를 해결하지 못하면 다른 문제는 더욱 해결 하지 못할 것 같은 오기가 생겨 이 문제를 먼저 해결하기로 다짐했습니다.

처음 이 문제를 접했을 때 컴퓨터 처럼 앞에서 부터 차례로 계산 하지 않고 앞 과 뒤의 경우를 모두 따졌습니다. 그 결과 앞에서 계산한 바텀-업 방식을 활용하지 못하여 경우의 수를 통한 점화식을 찾아내지 못했습니다.

또한 값을 저장하는 dp가 과연 그 i번째 인덱스에서 최대값인지 의문이 들어 일일이 확인하느라 시간이 오래 걸렸습니다.

다른 풀이 (틀림)

저는 처음 정답인 점화식을 세우고도 기저와 반복문을 잘못 설정하여 틀렸습니다. 그런데 그 점화식을 고치지 않고 순간의 dp에 저장된 최대값이 잘못되었다고 생각하여 조금은 다른 방법으로 접근하여 새로 풀었습니다. 여기서 시간이 많이 걸렸습니다.

접근 방식은 다음과 같습니다.

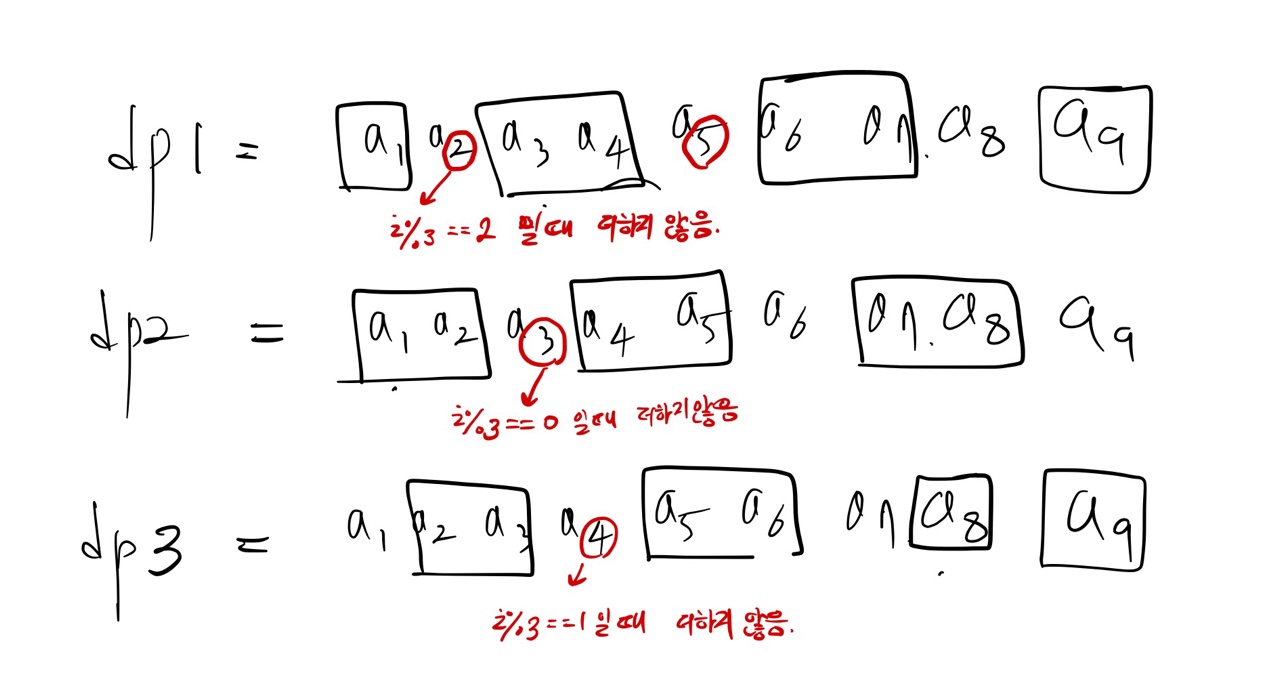
먼저 이전에 계산한 작은 값들을 저장할 리스트를 3개를 만들었습니다. 그리고 각 리스트 마다 규칙성을 찾아 누적을 저장하였습니다.

dp1 리스트는 인덱스를 3으로 나눌때 나머지가 2로 떨어지는 경우 값을 더하지 않았고

dp2 리스트는 3으로 나누어 떨어질 때 값을 더하지 않았습니다.

마지막으로 dp3 는 나머지가 1일 경우 더하지 않았습니다.

저는 이 경우를 각각 리스트를 선언해서 문제를 풀었습니다. dp를 하나만 선언하여 최댓값을 저장하는 과정에서 문제가 발생한다고 생각하여 따로 선언했습니다.

위 방식으로 파이참에서는 정상적으로 작동하고 모든 문제도 풀리긴 했지만 메모리 공간이 많이 소요되는지 백준에서는 틀렸습니다 가 출력되었습니다.

그래서 다시 문제를 리스트 하나로 제한하며 풀려고 노력했고 처음에 제가 새웠던 점화식으로 풀었더니 해결 되었습니다.

아래는 틀린 코드입니다. 시간복잡도 뿐만 아니라 공간복잡도, 메모리도 코딩테스트에서는 중요하다는 것을 새롭게 배우게 되었습니다.

n = int(input())

array = [0]*(n+1)

dp1 = [0]*(n+3)
dp2 = [0]*(n+3)
dp3 = [0]*(n+3)

for i in range(1, n+1):
    array[i] = int(input())

# 초기값 필요없음
#dp1[1] = array[1]
#dp2[2] = array[1] + array[2]
#dp3[3] = array[2] + array[3]

for i in range(1, n+1):
    if i%3 == 2:
        dp1[i] = dp1[i-1]
        dp2[i] = dp2[i-1] + array[i]
        dp3[i] = dp3[i - 1] + array[i]

    elif i%3 == 0:
        dp1[i] = dp1[i-1] + array[i]
        dp2[i] = dp2[i - 1]
        dp3[i] = dp3[i - 1] + array[i]

    elif i%3 == 1:
        dp1[i] = dp1[i-1] + array[i]
        dp2[i] = dp2[i - 1] + array[i]
        dp3[i] = dp3[i - 1]

print(max(dp1[n], dp2[n], dp3[n]))